[codestates] graph, tree, bst
Tree
tree 는 단방향 그래프 구조로, 계층적 자료구조이자 비선형구조입니다.
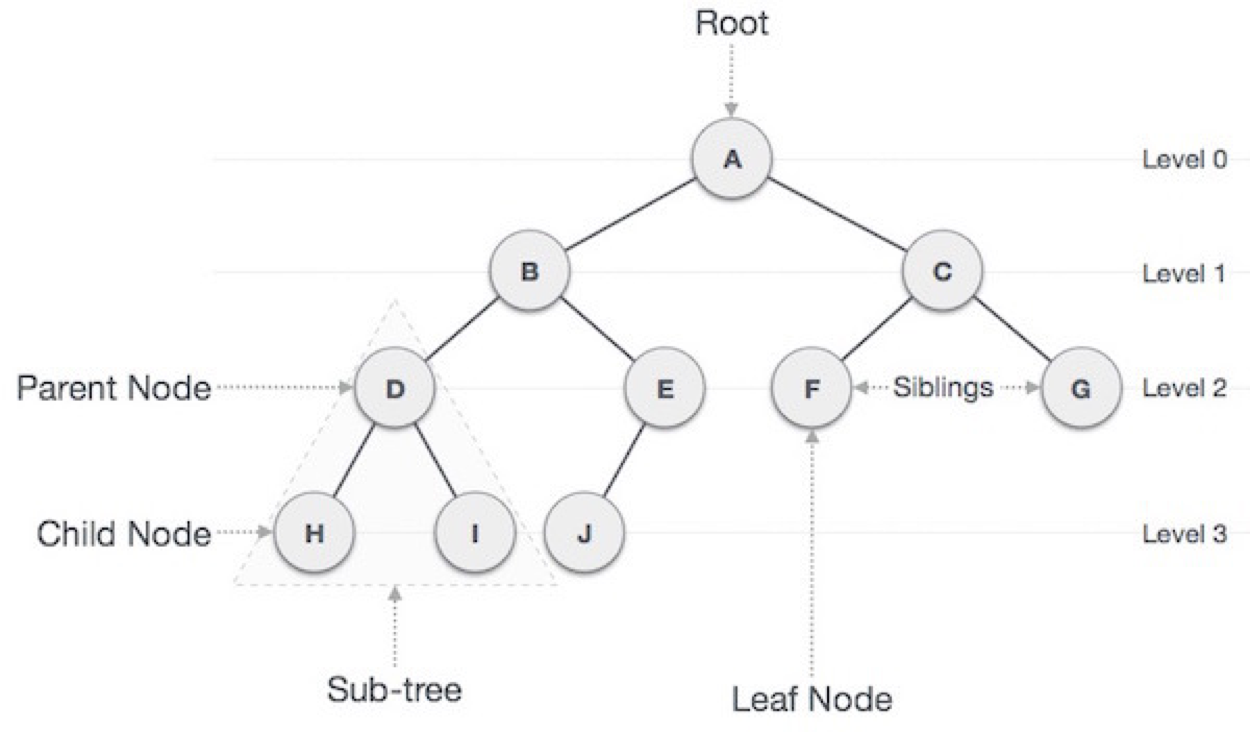
tree 의 장점은 다음과 같습니다.
- 효과적인 계층 구조 표현
- 정렬과 탐색에 활용
- 삽입과 삭제가 쉬움 : 삽입, 삭제 시 해당 노드의 부모와 자식 노드만 수정하면 됩니다.
- 구조 파악이 용이
BST(Binary Search Tree, 이진 탐색 트리)
BST 는 이진탐색 속성이 이진 트리에 적용된 특별한 형태의 이진트리입니다. 여기서 이진트리란 자식 노드가 최대 두개인 노드들로 구성된 트리를 말합니다.
이진탐색은 정렬된 데이터 중 특정한 값을 찾기 위한 탐색 알고리즘입니다. 이진탐색 알고리즘은 오름차순으로 정렬된 데이터를 같은 크기의 두 부분으로 나눈 후, 두 부분 중 탐색이 필요한 부분에서만 탐색하도록 탐색 범위를 제한하여 원하는 값을 찾는 알고리즘입니다. root 를 중심으로 작으면 왼쪽, 크면 오른쪽으로 이동하며 탐색합니다. 최대 트리의 높이(h) 만큼 탐색을 진행합니다.
BST 에 노드 추가
노드를 추가할 때도 탐색과 마찬가지로 현재 노드보다 작으면 왼쪽, 크면 오른쪽으로 추가합니다. 이 작업은 노드를 삽입하려는 위치까지 재귀적으로 탐색하며 이루어집니다.
BST 에 노드 삭제
-
삭제할 노드가 리프 노드일 경우
리프노드는 그냥 삭제하면 됩니다.
-
삭제할 노드의 자식 노드가 하나인 경우
삭제할 노드의 자식노드와 부모노드를 연결해주면 됩니다.
-
삭제할 노드의 자식 노드가 두 개인 경우
먼저 좌측 혹은 우측에 있는 자식노드와 삭제할 노드의 위치를 변경합니다. 이후 변경된 위치에서 1, 2, 3번을 재귀적으로 반복합니다.
Graph
그래프는 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료 구조입니다.
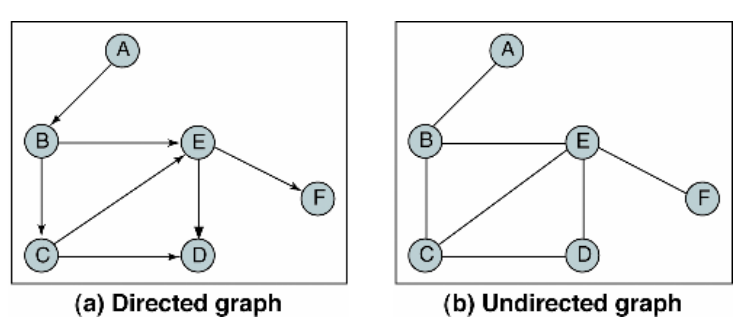
- 하나의 점을 그래프에서는 정점(vertex)이라고 표현하고, 하나의 선은 간선(edge)이라고 합니다.
Graph 의 표현 방법
인접행렬
인접행렬에서 이어져있다면 1, 아니라면 0 으로 표시합니다.
int[][] matrix = new int[][]{
{0, 0, 1}, // A -> C
{1, 0, 1}, // B -> A, C
{1, 0, 0}. // C -> A
};
인접리스트
인접 리스트는 각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 표현합니다. 각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있습니다.
// A, B, C는 각각의 인덱스로 표기합니다. 0 == A, 1 == B, 2 == C
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
graph.add(new ArrayList<>(Arrays.asList(2, null)));
graph.add(new ArrayList<>(Arrays.asList(0, 2, null)));
graph.add(new ArrayList<>(Arrays.asList(0, null)));
graph.get(0) == [2, null] == 0 -> 2 -> null
graph.get(1) == [0, 2, null] == 1 -> 0 -> 2 -> null
graph.get(2) == [0, null] == 2 -> 0 -> null
B 에서 A, C 로 이어지는 간선의 순서는 보통 중요하지 않습니다. 인접리스트는 메모리를 효율적으로 사용하고 싶을 때 사용합니다. 인접 행렬은 연결 가능한 모든 경우의 수를 저장하기 때문에 상대적으로 메모리를 많이 차지합니다.
Graph 용어
- 정점 (vertex): 노드(node)라고도 하며 데이터가 저장되는 그래프의 기본 원소입니다.
- 간선 (edge): 정점 간의 관계를 나타냅니다. (정점을 이어주는 선)
- 인접 정점 (adjacent vertex): 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점을 뜻합니다.
- 가중치 그래프 (weighted Graph): 연결의 강도(추가적인 정보, 위의 예시에서는 서울-부산으로 가는 거리 등)가 얼마나 되는지 적혀 있는 그래프를 뜻합니다.
- 비가중치 그래프 (unweighted Graph): 연결의 강도가 적혀 있지 않는 그래프를 뜻합니다.
- 무향(무방향) 그래프 (undirected graph): 각 노드의 간선에 방향이 없는 그래프입니다. 방향이 있으면 단방향(directed) 그래프입니다.
- 진입차수 (in-degree) / 진출차수 (out-degree): 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지를 나타냅니다.
- 인접 (adjacency): 두 정점 간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점입니다.
- 자기 루프 (self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다라고 표현합니다. 다른 정점을 거치지 않는다는 것이 특징입니다.
- 사이클 (cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현합니다.



댓글남기기